INTRODUCTION.

With the range of atmospheric dispersion models now available effort has been made in the past few years to develop means of validating and comparing the models. The BOOT methodology, developed by Hanna et al. (1991) and circulated by Helge Olesen (1994a, b), is now widely used under the title of ‘Model Validation Kit’ (MVK) (Olesen, 1998). This is a well defined procedure but, in its commonly presented form, is somewhat simplistic.

In view of the significant improvements in the modelling of atmospheric dispersion over the past decade, John Irwin of the USEPA has sought to develop a more sophisticated methodology. This has resulted in the production of a draft ASTM validation protocol (Irwin, 1999) with an accompanying computer code known as ASTM90. It is likely that, once approved, the ASTM90 protocol will be used by many to determine the relative performance of atmospheric dispersion codes.

Near-surface concentrations are the values of main interest in most atmospheric air pollution assessments, and are the most available observations. Therefore, throughout this report ‘observations’ and ‘concentrations’ refer to near-surface values.

Commercial models which simulate atmospheric dispersion all assume that the plume disperses downwind of the site with Gaussian characteristics in the horizontal and vertical lateral spreading.

Thus in the cross-wind (y) direction:

C(y) = C_max exp (-y²/2s _y) (1)

where s _y is the lateral standard deviation and C_max is the concentration on the centreline.

In all cases the assumed plume centreline is taken to be directly downwind form the source (though the calculation of the ‘downwind direction’ itself depends on the assumptions about the vertical variations in the wind profile, and normally ignores Ekman spiral effects). Both the MVK (BOOT) and ASTM validation methodologies ignore the plume direction and, where required, assume that the model uses the correct direction. This assumption neglects information which could contribute to assigning confidence to model results.

In the limited number of model data sets used for validation (see Table 1) a common feature is that significant concentrations can be observed at large angles from the centreline. One consequence of this is the user needs to determine what is the appropriate downwind distance to use for a given angle - is it the radial (r₀) or the downwind (x₀) value.

Table 1: List of observational data sets used for validation of Atmospheric Dispersion Models

The observed values in the data sets listed in Table 1 vary over orders of magnitude (and, of course, include observed values of zero). Because of this it is recognised (Hanna et al, 1991) that the mean of a set of values might not be the most appropriate representative value, as it could be dominated by a few observations. To allow for this the BOOT package provides the user with the choice of using the observed values or their logarithm in the analysis - using the latter is equivalent to testing against the geometric mean (GM) instead of the more normal arithmetic mean (AM). However, this option is rarely used despite its recommendation by Hanna et al (1991, p25)

Figure 1: Illustration of the ambiguous definition of distance to off-axis observation.

The ‘Model Validation Kit’ (MVK) is a well-established validation procedure, used by many code developers to illustrate how well their model does. It is often referred to as the BOOT package, but for the reasons given below it is here referred to as the Model Validation kit (MVK).

The basis of the MVK methodology is the work of Hanna et al. (1991), who used a Bootstrap resampling approach to estimate the confidence limits on some of the output parameters. The methodology, and associated ‘BOOT’ code, has been circulated by Helge Olesen (1994a) of NERI and is now widely used under the title of ‘Model Validation Kit (Olesen, 1998). The main products of the MVK (BOOT) package which are normally presented by users (e.g. Carruthers et al, 1998) are either as tables of observed and modelled data or as graphs (Scatter plots; Quantile-Quantile (QQ) plots; Box plots of modelled divided by observed concentrations, etc.)

The values normally presented in the table are Mean, Sigma, bias, NMSE, Cor, FA2, Fb and fs. Their definitions are given by Table 2:

Table 2: Definition of the parameters tabulated in the MVK standard output.

Additionally there is an option in BOOT to undertake a further statistical analysis giving the ‘robust’ and ‘seductive’ confidence limits, student t-test value, mean, standard deviation for the mean of the observations, and for NMSE, FB and Cor for comparison between model and observation, and inter-model comparison. It is for these latter, and little used, results that the Bootstrap approach is used by the code. For these reasons it is more appropriate to refer to the methodology normally used as MVK rather than as BOOT.

Scatter plots produced by the MVK are of all the observations and a model’s predictions. Often the scatter plots are very scattered. Because of the large amount of scatter it is more common for the Quartile-Quartile plot to be analysed.

In Quantile-Quantile (QQ) plots the observational and modelling data are each ordered from highest to lowest. Then the corresponding values are plotted. The resultant plot is, by definition, monotonic. Any systematic deviation from the line x = y is taken to indicate a bias in the model. A common feature is for a model to give good agreement, except for the largest few observations which are underestimated by the model.

The other commonly presented form of graphical output from the SIGPLOT package are box plots of C_p/C_o (modelled divided by observed concentrations). These can be plotted against any specified input parameter, such as distance, wind speed, mixing height, time of day etc. The user can specify the box size, though normally these box plots use the 5th, 25th, 50th, 75th and 95th percentiles.

The MVK has been widely used, by more than 100 research groups (Olesen, 1998). The MVK output (tables and graphs) are regularly used by modellers to assess their own models and to compare with other models (see, for instance, IJEP 1995; IJEP , 1997). The MVK has been a valuable resource in quantitatively assessing the performance of atmospheric dispersion models.

Initial analyses considered the full range of MVK output, including the use of the bootstrap results to give estimate of confidence limits (e.g. Olesen, 1995, Figure 2). However, the tendency has developed for the MVK users to focus on the summary table output, and on the Scatter, QQ and box plots for presenting their results. These present a simplified analysis of model performance, ignoring many of the relationships between the data which might provide useful additional information. For instance, the results (both the arithmetic mean and the scatter/QQ plots) are most influenced by the largest values.

The MVK basis its calculations on a single value for each arc of each experiment, the maximum observed concentration (C_mac). This value is easily derived from the observational data set, though due to variations in data quality such values have, for some data sets, subsequently been annotated with an estimated ‘Quality’ - a number in the range 0 to 3, derived from visual inspection of the data.

The bias introduced by this definition has been subject of some discussion (Irwin and Lee, 1995; Irwin, 1999; Olesen, 1998). Olesen (1998) compares the performance of the MVK using maximum arcwise concentrations (MAC) with the near-centreline concentrations (NCC) introduced by Irwin (1999). One difference seen between the MAC and NCC approaches is that the latter give much lower averages. Olesen’s (1998) Figure 4 shows that a model with a good fit when the MAC methodology is used will have a poor fit with Irwin’s NCC methodology.

One aspect where the NCC methodology is clearly better is in the prediction of zero values - whilst by definition there are no zeros in the MAC data set, there are some in the (fuller) NCC data set, and thus, as the OML model sometimes predicts zero concentration, the results closer to the origin are improved. (See Figure 4 in Olesen, 1998).

In earlier work (Irwin and Lee, 1995) a means of deriving the cross wind integrated concentration, the lateral standard deviation (s _y) and from these the estimated peak concentration (C_max) were derived (see Equation 3 below). It would be very worthwhile comparing the results of using C_max against those of using MAC and NCC. It should be noted that the initial impetus for introducing the concept of the NCC was to produced multiple values for input to the ASTM methodology, as they would give a better estimate of the variability of results. In contrast to this C_max was developed as a ‘best estimate’ of the peak concentration, and therefore is more appropriate to the MVK approach.

A standard component of the application of the MVK is the use of QQ plots (see Olesen, 1995, Figures 4, 9 and 12; Carruthers et al, 1998, Figures 2 and 3). Whilst QQ plots show model performance there is no theoretical justification for independently ordering the model and observational data in this way. Normally even for the highest values the model and observations are taken from different experiments. (For instance, in Figure 2 of Carruthers et al, 1998, the highest 10 model concentrations are from a completely different 10 experiments than the highest 10 observations.) Also, in the centre of the ordering there is a mixing of values from different downwind distances.

My opinion is that QQ plots, as produced by the MVK, are not a valid means of presenting the results. Two (related) changes are required so that the pooling of data used in QQ plots can be justified on a theoretical basis. These changes are to restrict the pooling to data from the same distance and stability regime as is done in the ASTM methodology. Once the observations and modelled results have been separated into distance/regime categories then the values within these categories could be reordered for QQ plots using the same justification as is used in ASTM. The resulting plots would obviously be expected to have a spread of data points somewhere between the existing scatter and QQ plots.

As referred to in Section 2, the Boot package of Hanna et al (1991) includes the option of analysing the data using the observed values or their logarithm. The latter is equivalent to testing against the geometric mean (GM) instead of the more normal arithmetic mean (AM). However, this option is rarely used despite its recommendation by Hanna et al (1991, p25). Hanna et al (1991) define two additional variables: MG (the Mean geometrical Bias) and VG (geometric mean variance).

The BOOT package allows for four alternate performance measures:

1. Straight C_o and C_p, with no normalisation;
2. C_o and C_p, normalised by C_o;
3. C_o and C_p, normalised by C_p;
4. ln(C_o) and ln(C_p).

For the first three options FB and NMSE (see Table 2) will be calculated, whilst in the fourth case MG and VG are used. Hanna et al (1991, p27) analyse the option as:

1. Emphasis on high observed and/or predicted concentrations;
2. Emphasis on large overpredictions, independent of magnitude;
3. Emphasis on large underpredictions, independent of magnitude;
4. Balanced emphasis.

It can therefore be seen that the normal application of the MVK emphasises high observed and/or predicted concentrations. This focus is reinforced by the scatter and QQ plots by the use of linear rather than logarithmic axes. There would, therefore, be greater concern about the underestimate of the maximum by 10%, than the overestimate of half the values by a factor of 2. Which should be of greatest concern depends on the context, but here the important point is that the user may have inadvertently focused on the highest values.

The draft ASTM methodology is still under development (Irwin, 1999), and is at present being assessed by modellers (e.g. Olesen, 1998). It assumes that the statistical evaluation of a (dispersion) model is only part of a larger process, model evaluation.

The latest version of the draft ASTM methodology is described in Irwin (1999), and is summarised below.

One important component of the ASTM methodology is the idea of stratifying the model evaluation data into selected regimes (Lee and Irwin, 1994). This was first undertaken in Irwin and Smith (1984) who considered 2 stability strata (night and day) and two distance strata (less than and greater than 11 km). It has subsequently been applied by (Lee and Irwin, 1994) and now in ASTM. A common stability stratification is into four regimes (Very Unstable, Unstable, Stable, Very Stable). Analysis by Irwin and Lee (1995, Figure 1) showed that this was indeed a sensible means of splitting the data from Prairie Grass, with the dispersion being governed by the Monin-Obukhov length.

The primary goal is to use as few strata as needed to capture the essence of the physics being characterised, such that model bias can be quantified. Another consideration in defining the strata is that there should be a reasonable number of arcs of data within the strata (Irwin, 1999, suggests at least 7). Analysis by stability category has revealed informative patterns of model bias a function of stability (Turner and Irwin, 1985; Carruthers et al, 1998).

Unlike the MVK approach, the draft ASTM methodology uses all the observations ‘close’ to the centreline, rather than just the maximum value. Lee and Irwin (1994) argue that the magnitude of natural variability was sufficient that the observed arcwise maximum concentration (MAC) values would tend to be significantly larger than the ensemble centreline concentration value. Thus a comparison of observed arcwise maximum with model estimate was deemed undesirable.

This suggestion was analysed in further detail in Irwin and Lee (1995) who calculate a Gaussian maximum concentration (C_max) for each individual arc by first determining the lateral dispersion Sy, by summing the squared distance from the local centre of mass, weighted by the observed concentration:

(2)

C_max can then be defined for a single experimental arc from the integral of Equation 1:

where (3)

where the modulus or r is used to increase accuracy in the integration.

Irwin and Lee (1995) used these results, combined with the ensemble mean values, to illustrate the scatter in observations (their Figures 4 to 6). These figure demonstrate the advantages in a validation process using multiple values from each observation arc.

The local centre of mass is computer for each arc and then Sy is calculated using Equation 2. The ‘near’ centreline concentrations are defined as coming from those locations within 0.67 standard deviations of the centreline, i.e. if |y| < 0.67 Sy. Before concentrations from different experiments can be combined they must be normalised by dividing by the emission rate.

The study by Irwin and Lee (1994, described in Section 4.1.2) showed that stochastic fluctuations (natural variability) in the concentration values within the near-centreline portion of dispersing plumes have a roughly log-normal distribution with a standard geometric deviation of order 1.5 to 2. Thus unbiased deterministic dispersion models are expected to underestimate the higher percentiles of the observed centreline concentrations. Thus in ASTM the observed feature for comparison with modelling results is the average of the values selected as being representative of centreline concentration values.

The statistic used for making comparisons of the observed and modelled values are the fractional bias (FB) and the absolute fractional bias (AFB). The FB is as defined as

(4)

(the same as in MVK, but with the sign reversed), whilst the AFB is the absolute value of the FB.

To provide an objective means of combining the data from different regimes the inverse variance weighting method is used (Irwin, 1999). The variances of FB and AFB for each regime are determined using bootstrap resampling methods, and then combined using inverse weighting:

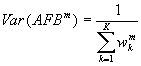; ; (5,6,7)

where superscript m refers to the model and subscript k to the regime.

Irwin (1998) presented results for the AERMOD, ISC and HPDM models for Prairie Grass, Kincaid and Indianapolis experiments. This lead to the conclusions that ISC has significant differences with observations in most of the comparisons made, HPDM appears better at tall stacks than for near-surface releases and AERMOD is the best of the models for near-surface releases and as good as HPDM for elevated sources.

These studies have shown the benefits of using the ASTM methodology:

1. Use of all near-centreline observations not just maximum. This could be further improved by correcting for distance from centreline as then a wider angle could be used (Irwin and Lee imply up to 2 Sy for Prairie Grass and Kincaid).
2. Stratification by distance so that values for different distances are not pooled together.
3. The stratification by stability also avoids mixing together results from different meteorologies, though there is no check on how consistent different observations within one regime were.
4. Clear intercomparison of various models, though there is a tendency to focus on a individual ‘best’ model even when there is not statistically difference..

In Table 1 of Irwin (1998) some of the limitations of the ASTM methodology can be seen. Two of the models (HPMD at Prairie Grass and ISC and Kincaid), have very high overall AFB values of 1.86 and 1.99 respectively, implying (weighted) average biases of a factor of 30 and 400 respectively. Associated with these high biases are very low standard deviations (0.002 and 0.001 respectively).

The reason for these (unexpected) results lies in the definition of the weighting and the overall system variance with the use of the Fraction Bias transformation: Unlike the raw data (or its logarithm) the Fraction Bias can lead to poor predictions being clustered close together (at a value of 2 if the observed is zero, or at -2 is the model gives zero), resulting in a low variance for poor results. However, the inverse variance weighting method assumes that a low variance means that the results can be given a high degree of confidence. Hence these poor results can be given a very high weighting in the calculation of the overall model AFB^m, and in the calculation of Var(AFB^m), leading to such an individual regime dominate the result. It should also be noted that the definition of Var(AFB^m) takes no account of the actual variation in AFB^m between the different regimes, indicating that this is not a ‘pooling’ of the results from the different regimes but a weighted average of the results.

Equation 6 is based on a dubious assumption - that all the fractional biases come from the same distribution. It is more normal practice (Topping, 1972) to calculate both the internal and external consistent error, and then to use the greater value. In ASTM this is likely to give a significant increase in Var(AFB^m).

(8)

The earlier work of Hanna et al (1991) emphasised the importance of considering the use of alternatives to the arithmetic mean. Later work has supported this:

1. Lee and Irwin (1994) advocate the use of log Cp and log Co, which relate more directly to Cp/Co.
2. Irwin and Lee (1995, Figures 7 to 10) showed that C/<C> was log-normal for Prairie Grass and Kincaid.
3. Irwin (1996, Figure 2) shows how the observed values over all stabilities at a fixed distance are close to a log-normal distribution.

However, the alternative geometric mean leads to difficulties when data (observed or modelled) is zero and hence consideration has been given to using quantiles, including the median and the 90th percentile (e.g. Irwin, 1996).

Subsequent studies by (Irwin and Rosu, 1998, fig 2) showed that, for Bootstrap samples, the arithmetic mean (AM) bootstrap sample is Gaussian (central limit theorem), but for Median and percentiles it is not. Therefore it was not so easy to define the variance in these case. That the AM gives a Gaussian shape is well known as the Central Limit Theorem. However, this leads to other difficulties (not recorded by Irwin and Rosu, 1998). In particular the representative values produced, and their distributions, are dominated by the largest few values. This therefore biases the observed distribution towards the maximum observed values. In view of the difficulties (described above) in defining the standard deviations even in the case of the AM, it would be worthwhile revisiting the feasibility of using alternative analysis methods, such as the median and quantiles.

The fraction bias (FB) is a non-linear operator which is used to represent the relative difference between model and observation in a bounded range (-2 to 2). When the model gives predictions within a factor of 3 of the observed values then the fractional bias result is very similar to the log of the ratio.

However, its non-linear nature means that the statistics of FB, such as the variance, can only be determined using sampling methods (e.g. bootstrap). Also, the bounded nature of the FB means that when the model grossly over or under predicts then the results are all very similar. This can lead to low standard deviations, which can be mistakenly be interpreted as implying a high level of confidence in the results. (See Section 4.1).

Caution therefore needs to be exercised when interpreting and combining results derived using the Fractional Bias transformation.

Whilst the current ASTM methodology only uses values within 0.67 S_y of the centreline, Irwin and Lee (1995) demonstrate the feasibility of using data (appropriately scaled) out to 2 S_y from the centreline. This would provide a much larger data pool, and might therefore make the analysis using medians and 90th percentiles, dismissed by Irwin and Rosu (1998) more justifiable.

Suggested improvements to MVK

1. Consideration of what observation to use. Try comparing C_max against C_MAC and C_NCC.
2. Produce QQ plots in which the data is only mixed within regime, not over distance or stability.
3. Consider use of geometric mean, MG, as suggested by Hanna et al (1991) when producing the Boot package.

Suggested improvements to ASTM90

1. Consider replacing FB with a (modified) log value (the modification being for zero values).
2. Correct the definition of standard deviation for overall data, to using Equation 8.
3. Consider use of median or geometric mean rather than arithmetic mean.
4. Consider using data over a wider range of angles but scaling up to an equivalent centreline value.

Carruthers D J, Dyster S and McHugh C A. (1998), Contrasting methods for validating ADMS using the Indianapolis dataset. Int J Environment and Pollution, in Press. [Rhodes conference paper.]

Hanna S R, Strimaitis D G and Chang J C. (1991), Hazard response Modeling uncertainty (A quantitative method), Sigma Res. Corp. Report

IJEP, (1995), ‘The workshop on operational short-range atmospheric dispersion models for environmental impact assessment in Europe’ 21-24 Nov 1994. Int J Environment and Pollution, 5, Nos. 4-6.

IJEP, (1997), ‘4th workshop harmonisation within dispersion modelling for regulatory purposes’, 6-9 May 1996. Int J Environment and Pollution, 8, Nos. 3-6.

Irwin J S, (1998), Statistical evaluation of atmospheric dispersion models, Int J Environment and Pollution, in Press. [Rhodes conference paper.]

Irwin J S, (1999), Standard Practice for Statistical Evaluation of Atmospheric Dispersion Models, Draft3. ASTM Designation Z6849Z.

Irwin J S and Lee R F, (1995). ‘Comparative evaluation of two air quality models: Within-regime evaluation statistic’. [Unpublished]

Irwin J S and Smith M E, (1984). ‘Possible useful additions to the rural model performance evaluation’, Bull Am Met Soc., 65, 559-568.

Lee R F and Irwin J S (1994). ‘A methodology for a Comparative evaluation of two air quality models.’ Int. J Environment and Pollution 5, no 4-6.

Olesen H R, (1995), The model validation exercise at Mol: overview of results, Int J Environment and Pollution, 5, p761-784.

Olesen H R, (1998), Model Validation Kit - status and outlook, Int J Environment and Pollution, in Press. [Rhodes conference paper.]

Topping J, (1972) Errors of Observation and their treatment, 4th Edition, Chapman and Hall.

Turner D B and Irwin J S, (1985), The relation of Urban model performance to stability. Air Pollution Modeling and its application IV, C De Wispelaere, ed. Plenum Pub Corp. New York, 1985, pp721-732.